Which Arctic Animals Love Math 9.12 Solving Absolute Value Equations And Inequalities Awnsers
The Globe's Most Cute Equations
Introduction

Mathematical equations aren't just useful — many are quite beautiful. And many scientists admit they are oftentimes fond of detail formulas not only for their function, merely for their class, and the simple, poetic truths they incorporate.
While certain famous equations, such as Albert Einstein'south Eastward = mc^two, hog most of the public celebrity, many less familiar formulas accept their champions among scientists. LiveScience asked physicists, astronomers and mathematicians for their favorite equations; here's what nosotros constitute:
General relativity
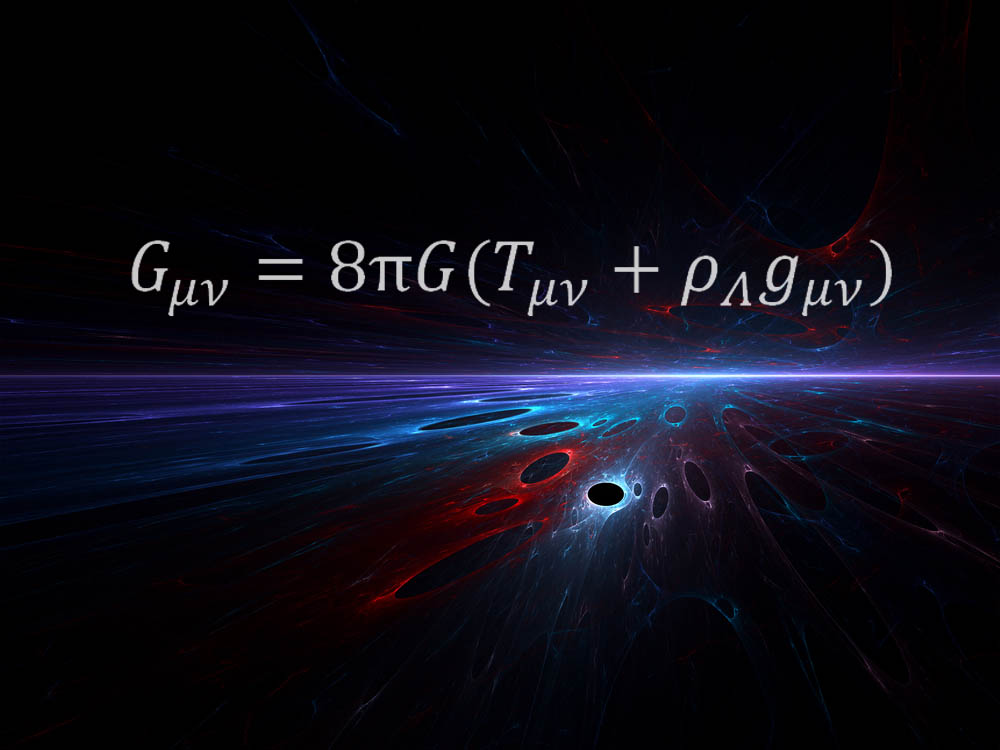
The equation above was formulated by Einstein as part of his groundbreaking general theory of relativity in 1915. The theory revolutionized how scientists understood gravity by describing the force as a warping of the material of space and fourth dimension.
"Information technology is still astonishing to me that 1 such mathematical equation tin describe what infinite-time is all about," said Infinite Telescope Science Establish astrophysicist Mario Livio, who nominated the equation as his favorite. "All of Einstein's truthful genius is embodied in this equation." [Einstein Quiz: Test Your Knowledge of the Genius]
"The right-hand side of this equation describes the energy contents of our universe (including the 'dark energy' that propels the current cosmic acceleration)," Livio explained. "The left-hand side describes the geometry of space-time. The equality reflects the fact that in Einstein's general relativity, mass and energy determine the geometry, and concomitantly the curvature, which is a manifestation of what we call gravity." [6 Weird Facts About Gravity]
"Information technology'southward a very elegant equation," said Kyle Cranmer, a physicist at New York Academy, calculation that the equation reveals the human relationship between space-time and affair and energy. "This equation tells you how they are related — how the presence of the sun warps space-fourth dimension so that the Globe moves around it in orbit, etc. It also tells you how the universe evolved since the Big Bang and predicts that there should be black holes."
Standard model

Another of physics' reigning theories, the standard model describes the drove of fundamental particles currently thought to make up our universe.
The theory can be encapsulated in a principal equation called the standard model Lagrangian (named later the 18th-century French mathematician and astronomer Joseph Louis Lagrange), which was called by theoretical physicist Lance Dixon of the SLAC National Accelerator Laboratory in California as his favorite formula.
"Information technology has successfully described all simple particles and forces that we've observed in the laboratory to date — except gravity," Dixon told LiveScience. "That includes, of course, the recently discovered Higgs(like) boson, phi in the formula. Information technology is fully self-consistent with quantum mechanics and special relativity."
The standard model theory has not yet, even so, been united with full general relativity, which is why it cannot describe gravity. [Infographic: The Standard Model Explained]
Calculus
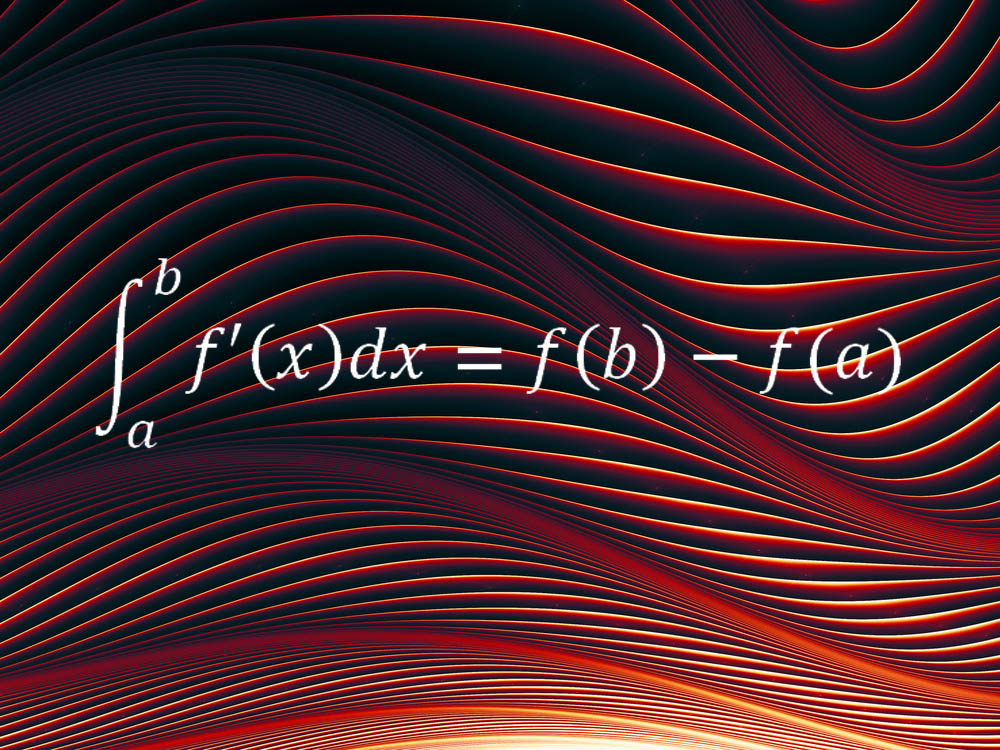
While the first 2 equations describe detail aspects of our universe, another favorite equation can be applied to all manner of situations. The fundamental theorem of calculus forms the backbone of the mathematical method known as calculus, and links its two main ideas, the concept of the integral and the concept of the derivative.
"In simple words, [information technology] says that the cyberspace modify of a shine and continuous quantity, such as a distance travelled, over a given fourth dimension interval (i.e. the departure in the values of the quantity at the end points of the time interval) is equal to the integral of the rate of change of that quantity, i.e. the integral of the velocity," said Melkana Brakalova-Trevithick, chair of the math section at Fordham University, who chose this equation as her favorite. "The fundamental theorem of calculus (FTC) allows us to determine the net change over an interval based on the rate of modify over the entire interval."
The seeds of calculus began in ancient times, but much of it was put together in the 17th century by Isaac Newton, who used calculus to depict the motions of the planets effectually the sun.
Pythagorean theorem

An "oldie but goodie" equation is the famous Pythagorean theorem, which every beginning geometry student learns.
This formula describes how, for any right-angled triangle, the square of the length of the hypotenuse (the longest side of a right triangle) equals the sum of the squares of the lengths of the other two sides.
"The very commencement mathematical fact that amazed me was Pythagorean theorem," said mathematician Daina Taimina of Cornell University. "I was a child then and it seemed to me and so amazing that it works in geometry and it works with numbers!" [5 Seriously Listen-Boggling Math Facts]
Euler's equation
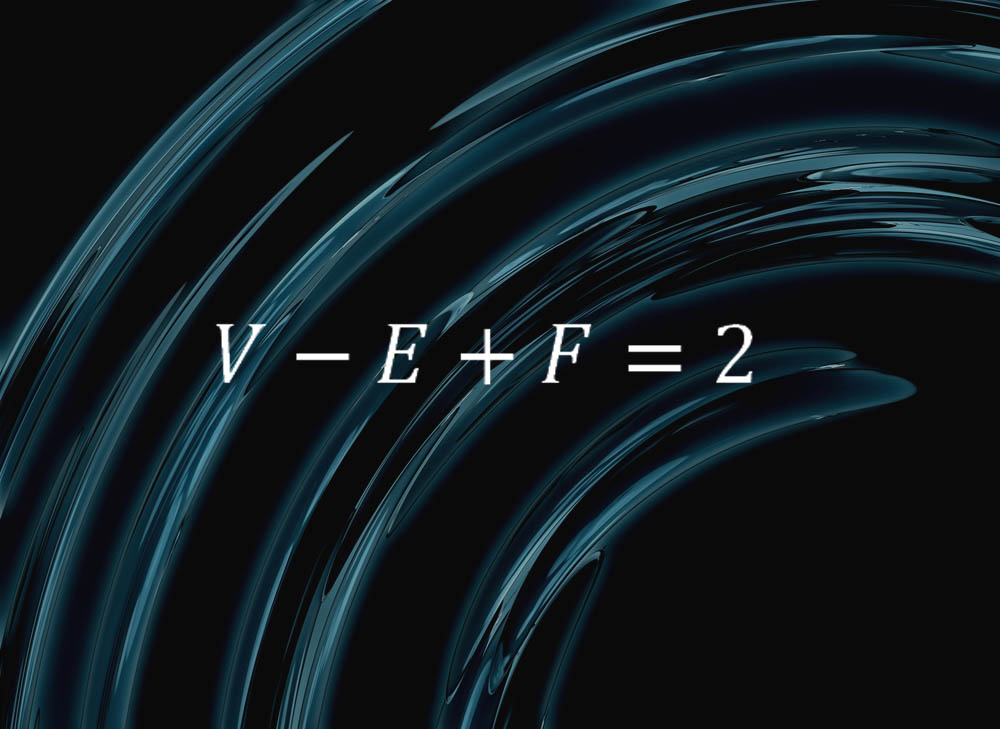
This simple formula encapsulates something pure about the nature of spheres:
"It says that if you cut the surface of a sphere up into faces, edges and vertices, and permit F be the number of faces, E the number of edges and V the number of vertices, you will always go Five – E + F = two," said Colin Adams, a mathematician at Williams College in Massachusetts.
"So, for example, take a tetrahedron, consisting of iv triangles, six edges and four vertices," Adams explained. "If you blew hard into a tetrahedron with flexible faces, y'all could circular it off into a sphere, so in that sense, a sphere can be cutting into four faces, six edges and four vertices. And nosotros meet that V – E + F = 2. Same holds for a pyramid with five faces — four triangular, and 1 square — eight edges and five vertices," and any other combination of faces, edges and vertices.
"A very cool fact! The combinatorics of the vertices, edges and faces is capturing something very fundamental about the shape of a sphere," Adams said.
Special relativity
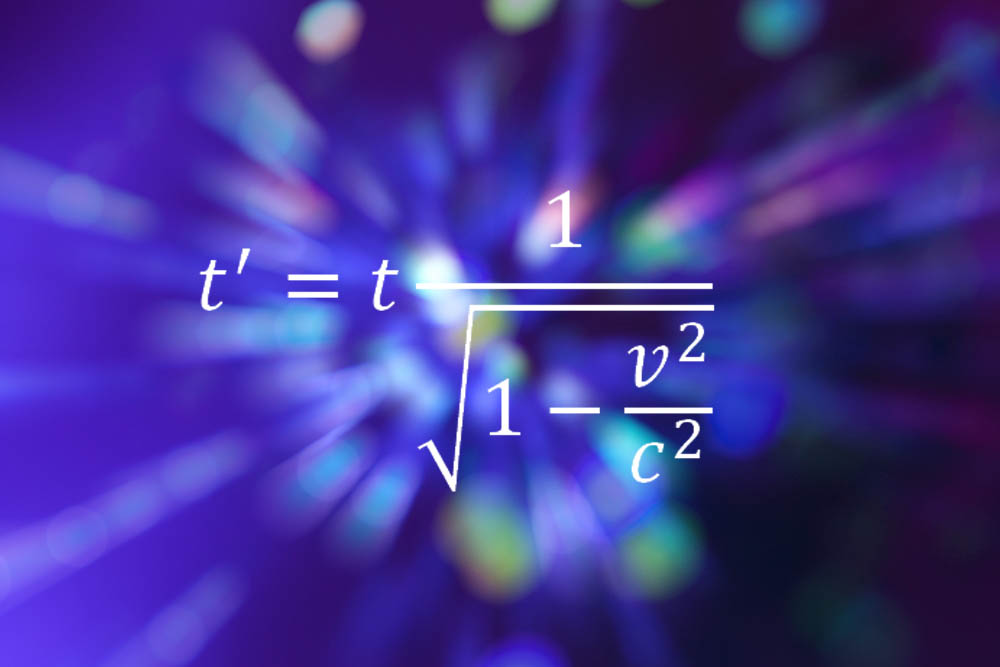
Einstein makes the list again with his formulas for special relativity, which describes how time and space aren't absolute concepts, but rather are relative depending on the speed of the observer. The equation higher up shows how fourth dimension dilates, or slows down, the faster a person is moving in whatsoever management.
"The point is it's actually very elementary," said Bill Murray, a particle physicist at the CERN laboratory in Geneva. "At that place is nothing there an A-level student cannot practice, no complex derivatives and trace algebras. But what it embodies is a whole new style of looking at the world, a whole mental attitude to reality and our relationship to information technology. Suddenly, the rigid unchanging cosmos is swept away and replaced with a personal earth, related to what you observe. Y'all motility from being outside the universe, looking downwards, to ane of the components inside it. Merely the concepts and the maths can be grasped by anyone that wants to."
Murray said he preferred the special relativity equations to the more complicated formulas in Einstein's afterwards theory. "I could never follow the maths of full general relativity," he said.
1 = 0.999999999….

This uncomplicated equation, which states that the quantity 0.999, followed by an infinite cord of nines, is equivalent to 1, is the favorite of mathematician Steven Strogatz of Cornell Academy.
"I love how simple it is — everyone understands what it says — yet how provocative information technology is," Strogatz said. "Many people don't believe it could be true. It's as well beautifully balanced. The left side represents the beginning of mathematics; the right side represents the mysteries of infinity."
Euler–Lagrange equations and Noether'due south theorem
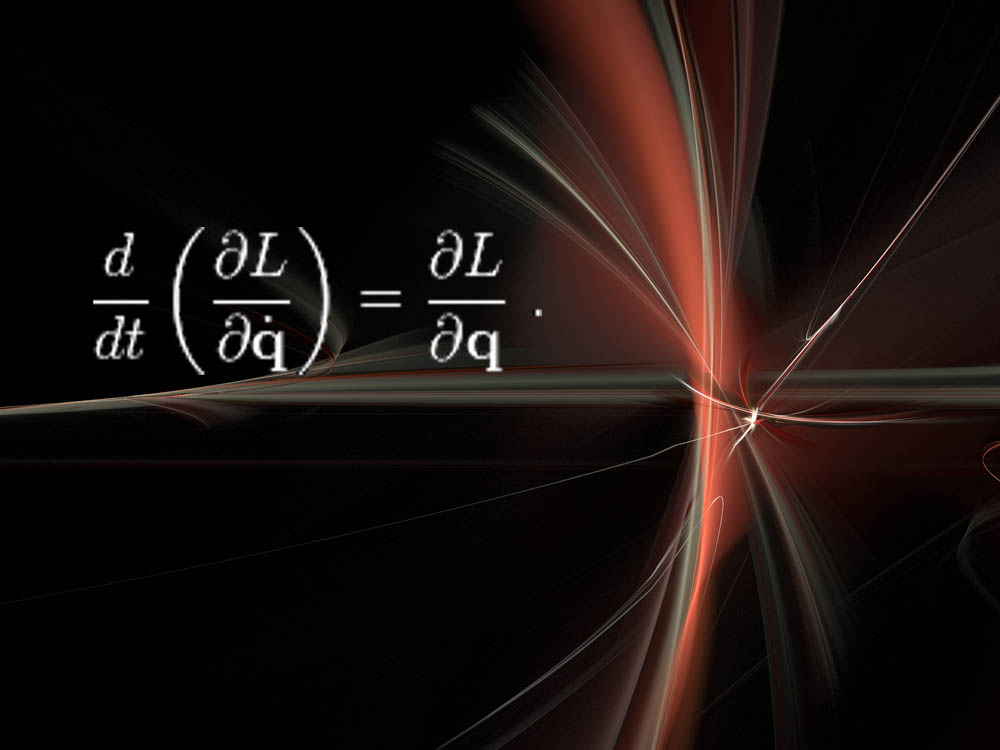
"These are pretty abstruse, just amazingly powerful," NYU's Cranmer said. "The cool matter is that this way of thinking almost physics has survived some major revolutions in physics, like breakthrough mechanics, relativity, etc."
Here, L stands for the Lagrangian, which is a measure of energy in a concrete arrangement, such as springs, or levers or key particles. "Solving this equation tells you how the system will evolve with fourth dimension," Cranmer said.
A spinoff of the Lagrangian equation is chosen Noether's theorem, after the 20th-century German mathematician Emmy Noether. "This theorem is really fundamental to physics and the role of symmetry," Cranmer said. "Informally, the theorem is that if your system has a symmetry, then there is a corresponding conservation police. For example, the idea that the cardinal laws of physics are the same today equally tomorrow (time symmetry) implies that energy is conserved. The thought that the laws of physics are the same here as they are in outer space implies that momentum is conserved. Symmetry is perhaps the driving concept in fundamental physics, primarily due to [Noether'due south] contribution."
Callan-Symanzik Equation
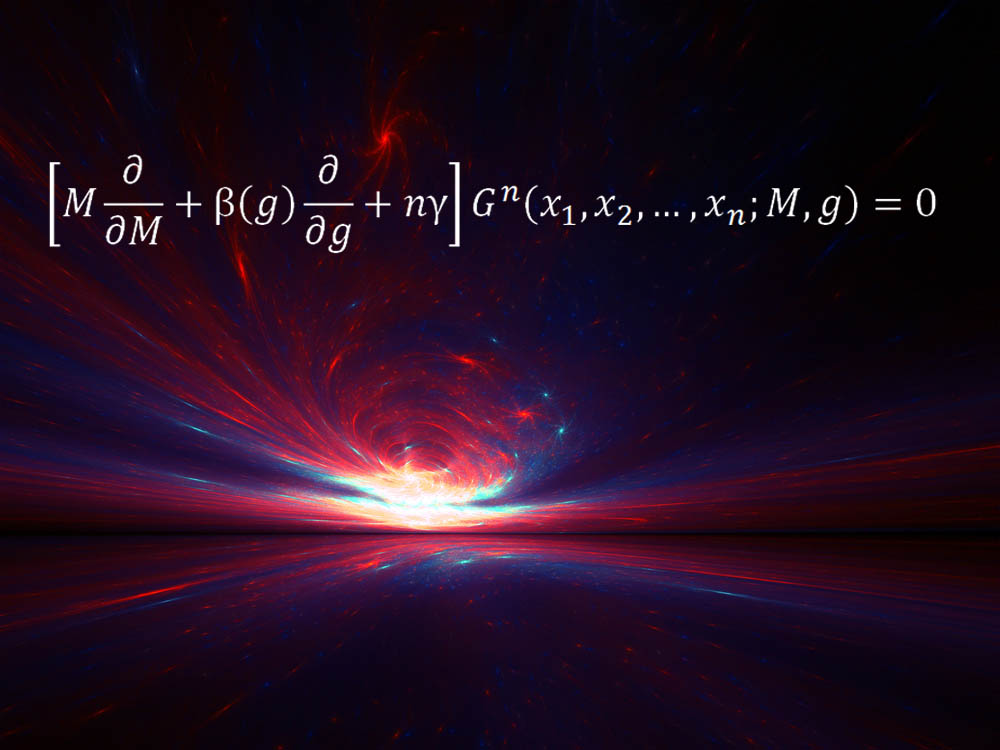
"The Callan-Symanzik equation is a vital first-principles equation from 1970, essential for describing how naive expectations volition fail in a quantum globe," said theoretical physicist Matt Strassler of Rutgers University.
The equation has numerous applications, including allowing physicists to estimate the mass and size of the proton and neutron, which make up the nuclei of atoms.
Bones physics tells us that the gravitational forcefulness, and the electrical force, betwixt two objects is proportional to the changed of the distance between them squared. On a simple level, the same is true for the strong nuclear strength that binds protons and neutrons together to form the nuclei of atoms, and that binds quarks together to class protons and neutrons. Withal, tiny breakthrough fluctuations tin can slightly modify a force's dependence on altitude, which has dramatic consequences for the strong nuclear strength.
"It prevents this force from decreasing at long distances, and causes it to trap quarks and to combine them to course the protons and neutrons of our globe," Strassler said. "What the Callan-Symanzik equation does is chronicle this dramatic and difficult-to-calculate outcome, important when [the altitude] is roughly the size of a proton, to more subtle but easier-to-calculate furnishings that tin be measured when [the distance] is much smaller than a proton."
The minimal surface equation
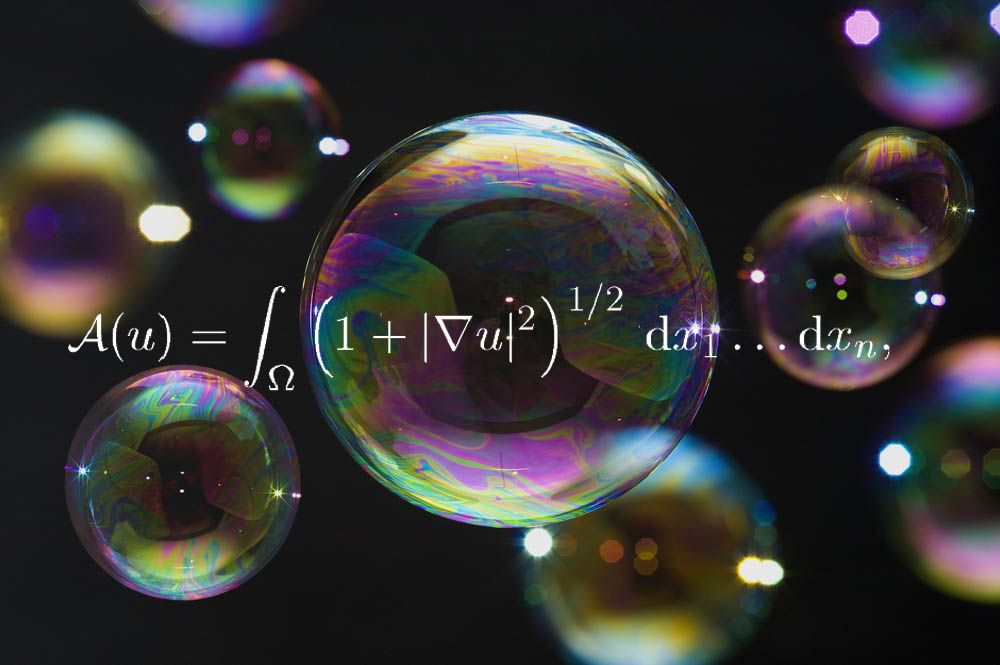
"The minimal surface equation somehow encodes the cute soap films that course on wire boundaries when you dip them in soapy h2o," said mathematician Frank Morgan of Williams Higher. "The fact that the equation is 'nonlinear,' involving powers and products of derivatives, is the coded mathematical hint for the surprising behavior of soap films. This is in contrast with more than familiar linear fractional differential equations, such equally the heat equation, the moving ridge equation, and the Schrödinger equation of breakthrough physics."
Source: https://www.livescience.com/26660-most-beautiful-mathematical-equations.html
Posted by: martinezthilvely.blogspot.com

0 Response to "Which Arctic Animals Love Math 9.12 Solving Absolute Value Equations And Inequalities Awnsers"
Post a Comment